Mean Time Between Failure (MTBF): Do we really understand it and is it an appropriate way to specify system performance?
Posted in Our news
May 2020
4 minutes reading time
I once had a tutor who would become apoplectic if any of his students used the terms reliability and MTBF in the same sentence; ‘There is little or no correlation between the two terms!’, he would shout. Putting the tutor’s very firm stance and opinion to one side, my experience in the world of reliability and support engineering over the past 30+ years has led me to question whether we, across industries and Users, really understand MTBF, whether it is really the most effective way to measure system performance and whether our reliance on it within requirements documents and design specifications is justified or wise.
Understanding MTBF – some simplified theory
Before attempting to answer these questions, it would be useful to understand what a Mean Time Between Failure is. As the name suggests MTBF is a Mean therefore it is derived using statistical techniques. Often, the less aware will simply divide the number of operating hours by the number of failures – this will provide a Mean, but the calculated statistical distribution will be a Normal Distribution. Most technical equipment does not fail ‘Normally’. Normal distributions were developed to describe human behavior. The common statistical distributions used when assessing technical failures are Lognormal, Weibull and Exponential and the calculations to derive means within these statistical distributions follow a broad technique, as follows (apologies to those who have not looked at their copy of Stroud for a few years):
- Gather the failure data – a dataset of at least 100 samples
- Classify the data into manageable chunks
- Plot the data points on statistical graph paper
- Least square regress the plotted curves to achieve a ‘best fit’ curve
- Assess the curves to hypothesize which is the most appropriate distribution
- Test the hypothesis using Kolmogorov – Smirnov
- Declare the distribution and measure the Mean.
There are, of course, computer programs that will do this for you in a very short time but I have always felt that understanding what the computer is doing for you helps you undertake the final stage of mathematical modelling – the human rationalization of the model output.
Having reached this point we should now understand that there are two important dimensions to the MTBF – the derived mean and the associated failure distribution.
Whilst talking about failure distributions there are some interesting characteristics of some distributions that are useful to understand:
- The mean of an Exponential Distribution is at approximately 63% on the distribution curve (not 50% as in the Normal) – the upshot of this phenomena is that 63% of equipment will have failed by the MTBF in an Exponential scenario.
- In an Exponential scenario we talk about a constant failure rate, which makes predicting failures difficult because they are random in nature.
- The failure mode of a single component whose failure is described by a Weibull distribution can be assessed by the shape parameter of the distribution – for instance, a shape parameter in the region of 2.75 to 3 might indicate a ‘wear out’ failure mode. However, when you combine several components into a system or system of systems, the scale parameter of the system level Weibull tends toward unity, which mimics the behavior of an Exponential distribution and we start to see random failures.
Specifying System Performance
Many requirements documents specify a MTBF as a measure of performance.
Immediately, I would ask the following questions:
- Do we really wish to specify system performance using a mean – is it appropriate for equipment to be averagely effective?
- Does specifying MTBF as a system performance requirement provide any guarantee of system performance?
To answer the first question we should consider what, for instance, a requirement statement that says ‘MTBF of 1000 hours’ really means. Firstly, it says that on average the User requires the equipment to fail no more frequently than after 1000 hours of operation. We know that failures will be distributed over the life of the equipment and some will fail before 1000 hours and some will fail after. Should we be content with that equipment which failed before 1000 hours in the knowledge that others will operate beyond? Secondly, as we have postulated earlier, 63% of our equipment may have failed by the MTBF. Do the requirements managers understand what MTBF really means? Is the User content that 63% of the equipment has failed by MTBF?
I would suggest that the User is more interested in the number of times that a piece of equipment operates correctly when they come to use it. To be more precise how reliable it is? Reliability is expressed as a probability greater than zero and less than 1 or as a percentage and, significantly, one does not express reliability as an average because equipment is simply not ‘averagely reliable’.
Dealing now with the second question. Specifying MTBF as a system performance parameter gives absolutely no guarantee of in-service system performance. During test and evaluation activity is the time to confirm that system requirements have been met. Simply, unless your test and evaluation program has tested to failure at least a hundred pieces of equipment there is insufficient statistical data to support any MTBF claims. Further, in order to ensure that any MTBF claims remain valid an in-service monitoring program may have to be invoked – all of which involves additional time and money.
Where a properly calculated MTBF can prove useful is in assessing the various availability parameters. The three academically accepted measures of availability are: Inherent; Achieved and Operational. These measures tell you almost all you need to know about system performance. There are other availability parameters used in Industry but the three quoted are the main ones. Inherent availability is a measure of equipment reliability and is a function of equipment failure and the time to repair it. Achieved availability incorporates the equipment preventive maintenance dimension and Operational availability adds measures of effectiveness of the support chain. There are mathematicians who try to overly complicate the calculations for each availability parameter but in their simplest form they are:
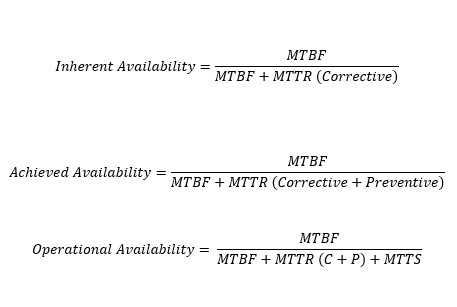
Where:
MTBF is a properly calculated Mean Time Between Failure
MTTR is a properly calculated Mean Time To Repair
MTTS is a properly calculated Mean Time To Support
Drawing on the foregoing it can be argued that, whilst specifying MTBF does not provide any guarantee of system performance, a properly calculated MTBF can be used to add clarity to system performance using availability parameters.
Final Thoughts
MTBF is a much used (and abused) parameter but it is only a mean and it should be used sensibly.
As a system performance measure MTBF is of little value and even less value if it is not calculated properly.
There is a host of information in a failure distribution if you look for it.
Availability parameters are much more useful and accurate system performance indicators giving us a view of reliability, maintainability and supportability system characteristics. MTBF is a useful supporting element to this dataset.
If you agree or disagree with my views, it would be great to hear from you.



